Generating complex, multi-biome procedural terrain with Simplex noise in PSWG

The magic at the core of Galaxies: Parzi's Star Wars Mod is adventure. In the Star Wars universe, there is every kind of biome imaginable: the barren ice tundras of the Hoth, the dry deserts and canyons of Tatooine, and the molten wastelands of Sullust, to name a few.

The adventure would be dull and boring if there weren't any planets to explore, but manually creating the terrain for each planet would be a colossal task requiring absurd amounts of time to create and to load into the game. Enter procedural generation.

Procedural generation makes it possible to simply define how the planet should look, and the world generation system will create a world each time that has the same general features but is, in itself, unique.

The mod's terrain generation framework is centered around a process we call Multi-Composite Terrain. At it's most basic level, it combines different kinds of terrain on a sliding scale of weights that determine the influence of a particular terrain generator at any position. Let's take a closer look at each step of the process.

The first step is to define different biomes' terrain generators. Above, for example, we can see a terrain generator for a series of navigable canyons for the player to explore, modeled loosely on the canyons on Tatooine. The generation script uses Worley noise to generate the canyon "cells," and uses Simplex noise in octaves to make the heightmap a little more interesting.

Each biome in the world needs to be defined independently, as its own heightmap function. Let's examine how each of these terrain generators is weighted in the world generator.

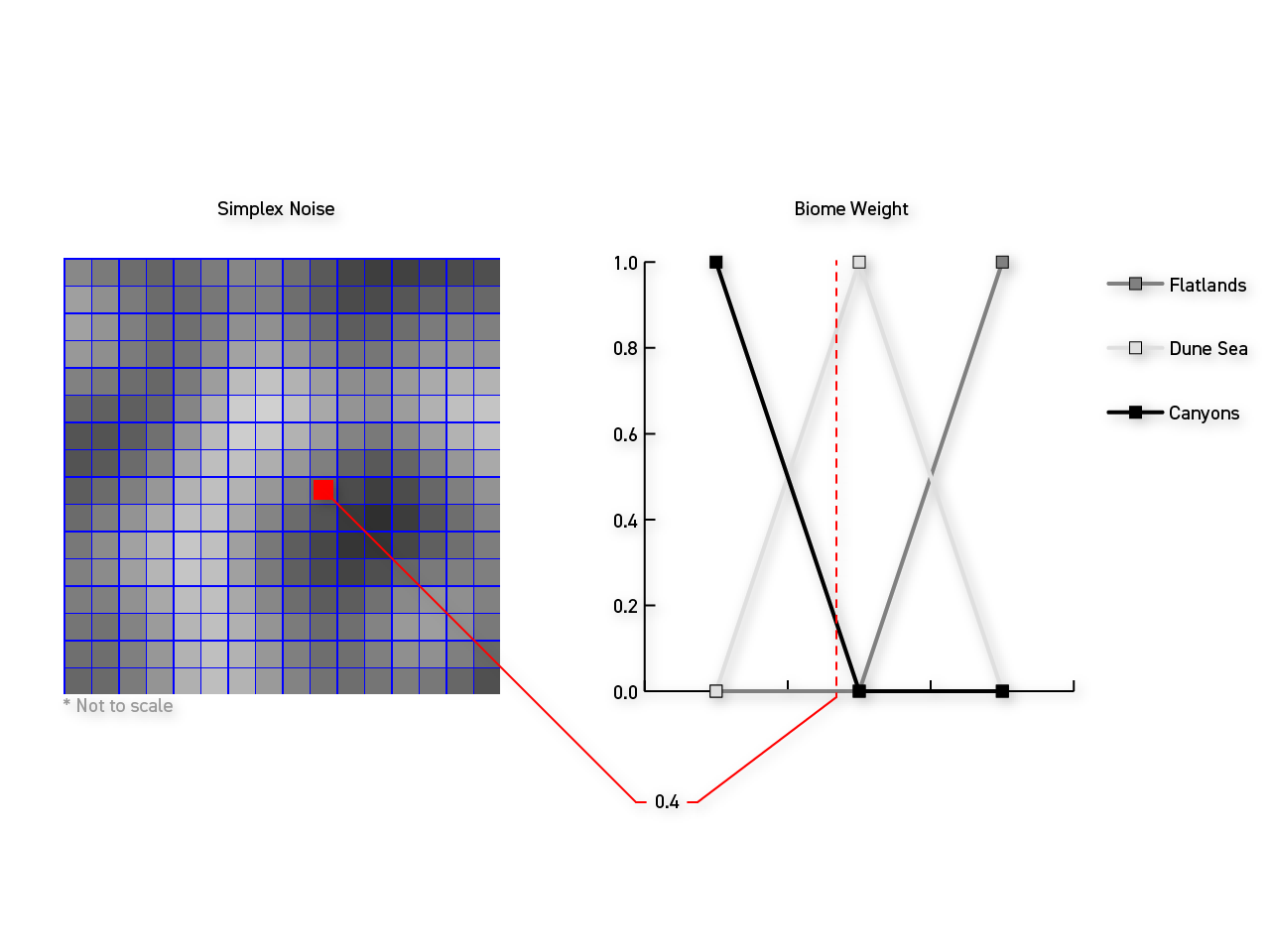
For each point on the heightmap, a "master" Simplex noise determines a single biome interpolation value for that point. Then, a weight function for each terrain layer determines the biome weights for that point using the previously calculated interpolation scalar. The weight function can be any function where the sum of the weights for all layers at \(x\) is equal to \(1\). My weight function is

\[-\left|\left(n-1\right)x-v\right|+1\]

where \(n\) is the number of layers (\(3\) in the above example) and \(v\) is the zero-based layer index within the system (\(0\), \(1\), and \(2\) for Canyons, Dune Sea and Flatlands in the example, respectively). You can find a Desmos graph for this function here if you'd like to tinker with the values. You should ensure no weight calculation results in a negative weight by discarding negative weights or adding a domain limiter to the weight function. In the example above, a noise value was selected at the position of the point on the heightmap. The value, \(0.4\), is then fed into the weight functions for each layer. The example results in a weight of roughly \(0.8\) for Dune Sea and \(0.2\) for Canyon.

The Java implementation of this biome weighting concept would look like:

double l = getMasterNoise(x, z);
double y = 0;
for (int i = 0; i < layers.length; i++)
{
	if ((i - 1f) / n <= l && l <= (i + 1f) / n)
		y += (-Math.abs(n * l - i) + 1) * layers[i].getHeightAt(x, z);
}

After all of the weights are calculated, a height is generated for each point in the heightmap for each layer, scaled by the weight, and added together to form the final height for that point.

As seen here at the "border" between a flatter region and a Canyon region, this method will create smooth, fluid transitions into different biome generation functions, where biomes are defined by weights are not as binary states. This completely eliminates the need for processing to remove ugly borders between two neighboring biomes. The cover image for this post also shows a transition of two biomes, a flatter sandy biome and a larger dunes biome, not explicitly mentioned here.